
Any vegetable seller is clear: the best way to put oranges, while occupying the least possible space – the so-called spherical packing problem – consists in forming a pyramid with them, in which each layer of oranges is placed on the holes of the bottom layer. But really, of all the possible arrangements of oranges, is this the one that makes the best use of space? The problem, which is more complex than it might seem, was only solved 25 years ago, and it took nearly 20 years to validate the answer.
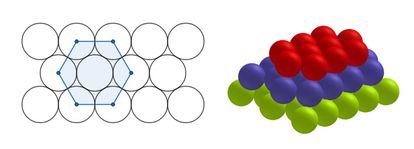
The problem was proposed in 1611 by the brilliant scientist Johannes Kepler. He predicted that in his two-dimensional version – which consists in determining the optimal way to place the circles on a plane – a similar arrangement of the pyramid in two dimensions – following a hexagonal pattern – was the optimal arrangement. The rigorous proof for this claim came in 1942, from Hungarian mathematician Laszlo Weijs Toth, who completed an incomplete proof by Axel Tho, proposed in 1890.
The problem of 3D spheres turns out to be more difficult. It wasn’t until 1998 when American mathematician Thomas C. in its presentation It also used some calculations that were made using computers, and the proof of the validity of these calculations was delayed until 2014.
Mathematicians have also studied high-dimensional packing, which also has applications in areas such as code debugging. If we treat every message (at most) 20 bits long as a header of a 20 dimensional cube, we can take advantage of good 20 dimensional spherical packages to correct the bad messages.
Specifically, if we receive a message that does not fit into our list of accepted messages – either because it doesn’t make sense or because we have a pre-defined list of messages that we consider acceptable – it could mean that there was a failure in the communication channel, and in such a case it would be fine Being able to correct it. To try to figure out what the initial message is, we can search for the message, among all the accepted messages, which is very similar to the one we received. To do this, simply compare the distances in the twenty-dimensional space of the letters.
Thus, if we have good encapsulation of the high-dimensional fields, we can interpret them as acceptable messages that allow debugging in the connection. The fact that it takes up such a small portion of space means that messages use the fewest possible number of bits.
However, the problem of optimal enclosures with higher dimensions – greater than three – remains an open one: only optimal configurations are found in the 8th dimension and the 24th dimension.

The result is in the eighth dimension has been shown in 2016 by Ukrainian mathematician Marina Vyazovska, who had just finished her PhD at the time. It is a very important milestone in modern mathematics because, in addition, its methods have simplified those used by Hales to prove the three-dimensional state. This does not mean, far from it, that the proof was easy: the work combines tools and techniques from Fourier analysis, number theory and field optimization. Furthermore, with his proof no arithmetic help was needed.
Through this publication, Viazovska quickly became famous all over the world and, together with other collaborators, Solve the problem in dimension 24 A year later, adapting the methods already used in the eighth dimension. However, these methods do not seem to work – without major modifications – for more dimensions, and no one has achieved definitive results in any other dimension yet. For some other dimensions, some of the current conjectures have been shown to be very close to optimal, but there are no complete proofs.
Will the field filling problem in some other dimension be resolved soon? This is already in the realm of speculation. But what we can be sure of is that, however interesting the result may arouse, the most fascinating thing about the proof in this sense is probably a profound new connection between the various fields of mathematics – as happened with Viazovska’s proof – which is always desirable to open the lines of new search.
Paul Hidalgo of Valencia He is a pre-doctoral researcher in ICMAT
Coffee and theories A section dedicated to mathematics and the environment in which it was created, coordinated by the Institute of Mathematical Sciences (ICMAT), where researchers and center members describe the latest developments in the discipline, share meeting points between mathematics and other social media and cultural expressions and remember those who marked their development and knew how to transform mathematics. Coffee to theories. The name evokes the definition of Hungarian mathematician Alfred Rainey: “A mathematician is a machine that turns coffee into theorems.”
Edition and Format: Agate A. Timón G Longoria (ICMAT).
You can follow MATERIA at FacebookAnd Twitter And Instagramor sign up here to receive Our weekly newsletter.

“Beeraholic. Friend of animals everywhere. Evil web scholar. Zombie maven.”
